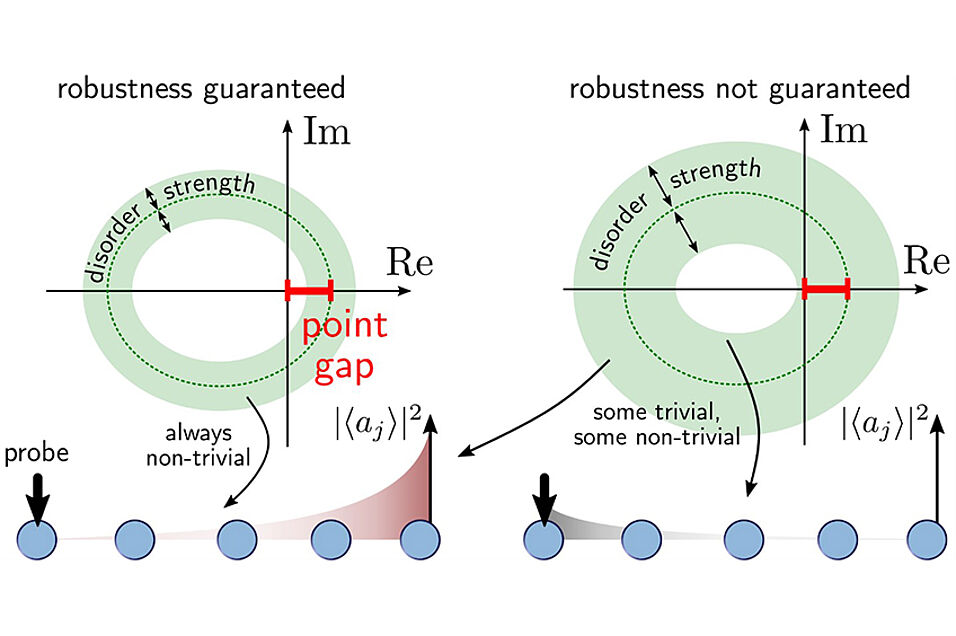
One of the most exciting properties of systems featuring non-trivial (Hermitian) topology is robustness against disorder. In recent years, studies have been extended to systems that experience gain and loss that are described by a non-Hermitian, rather than a Hermitian, matrix. Indeed, the same authors have shown that a non-trivial (non-Hermitian) winding number corresponds to directional amplification (Nat Commun 11, 3149 (2020)) which is potentially a key resource for quantum information processing. It has however remained unclear if systems featuring non-trivial non-Hermitian topology enjoy the same level of robustness against disorder as their Hermitian counterparts.
Writing in Physical Review Letters, the international team answers this question in the affirmative. They show analytically that the transport properties associated with non-trivial non-Hermitian topology are robust against disorder. This can be understood well graphically: Bounded disorder leads to eigenvalues within an annular region around the disorderless spectrum whose width is given by the disorder strength (green region). As soon as the annular region touches the origin, the disordered system may – with some probability – be topologically trivial and directional amplification is lost. Thus, directional amplification is robust as long as disorder does not close the point gap. The authors also show that non-reciprocity, i.e. suppression of transmission in the reverse direction is robust against even arbitrarily strong disorder.
Publication in Physical Review Letters:
Correspondence between non-Hermitian topology and directional amplification in the presence of disorder
Clara C. Wanjura, Matteo Brunelli, and Andreas Nunnenkamp
Phys. Rev. Lett. 127, 213601 (2021)
DOI: 10.1103/PhysRevLett.127.213601