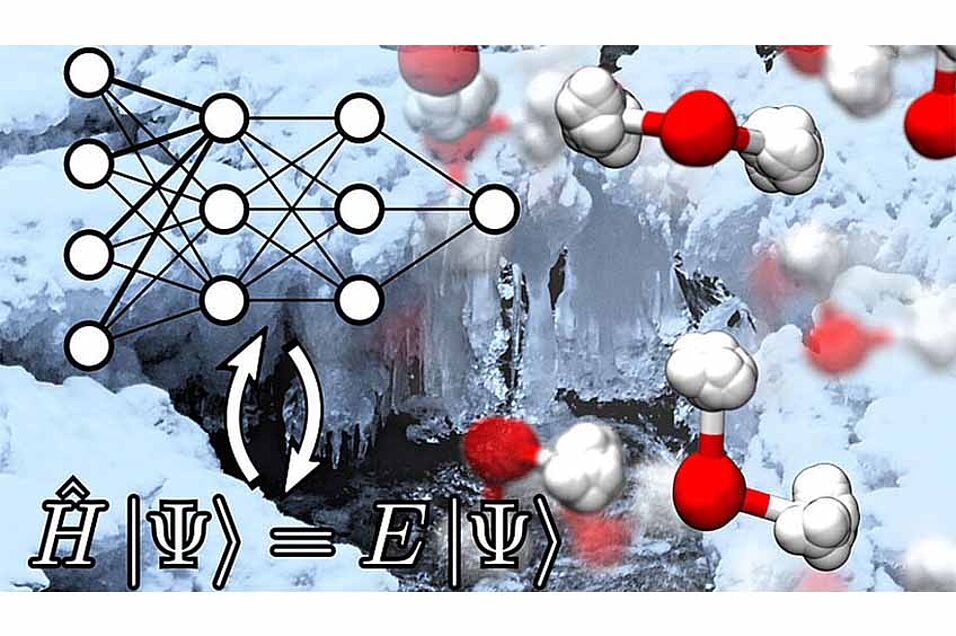
The building blocks of most observable matters are electrons and nuclei. Following the laws of quantum mechanics, their behavior can be described in terms of their wave function, sort of a diffuse cloud that is related to the probability of observing them in a given point and time. By solving the Schrodinger equation, it is possible to make models and predictions of any material, including water. But there is a catch. As the number of electrons and nuclei increases, the complexity involved soon become intractable even with the fastest supercomputers, and even after a century of celebrated progress in optimizing such calculations. In fact, quantum mechanical calculations are still unaffordable for systems with more than a few hundred atoms, or for a time period longer than a nanosecond, which is 1/1,000,000,000th of a second.
To overcome these harsh limitations, the researchers exploited an artificial neural network (ANN) to learn the atomic interactions from quantum mechanics. The architecture of ANNs can be represented as several layers of interconnected nodes, which mimics the structure of the neurons in a human brain. The ANN first learns quantum mechanical interactions between atoms, and then make speedy predictions about the energy and forces for a system of atoms, bypassing the need to perform expensive quantum mechanical calculations.
So far, it all rather sounds like a typical success story of machine learning. However, there are subtleties. The ANN has a residual error compared to the actual quantum mechanical calculations: most of the times it introduces a small noise, and sometime it makes a wild guess if an input is very different from anything it has learned. How to avoid the pitfalls of the ANN? Instead of employing ANN on its own to make predictions about a system of atoms, the researchers used it as a surrogate model. In essence, computing properties of materials at a finite temperature usually involves many computation steps, the laborious and repetitive parts can be delegated to the cheap surrogate model. Finally, the difference between the surrogate and the ground truth, which is the difference between the ANN and quantum mechanics, can be accounted for and subtracted from the final predictions.
With these techniques, the researchers were thus able to reproduce several thermodynamic properties of water from quantum mechanics, including the density of ice and water, the difference in melting temperature for normal and heavy water, and the stability of different forms of ice. Moreover, the study reveals several physical insights on what gives ice and water their peculiar properties. One of the most notable findings is the that nuclear quantum fluctuations, which is the tendency for light elements such as hydrogen to behave more like a diffuse cloud rather than a localized particle, promote hexagonal packing of molecules inside ice, which ultimately leads to the six-fold symmetry of snowflakes
Publication in Proceedings of the National Academy of Sciences of the United States of America:
“Ab initio thermodynamics of liquid and solid water”, Bingqing Cheng , Edgar A. Engel , Jörg Behler , Christoph Dellago , Michele Ceriotti, Proceedings of the National Academy of Sciences of the United States of America (2019).
Machine learning speeds up atomistic simulations of water and ice
08.01.2019